Related Posts:
In the previous post we covered the construction of the Gaussian Pyramid, followed by a brief overview of the procedure to construct the Laplacian Pyramid. In this post, we will relate the procedure to the application of blending two different surfaces, or images in the case of photography.
Blending procedure outline
A simple outline of the blending procedure, is as follows.
- Construct the Laplacian Pyramid for each image.
- Construct a Gaussian Pyramid for the mask.
- Apply the respective mask with the appropriate dimensions and blend the two images, repeating this step for each layer.
- Collapse the pyramid by expanding the layer with the smallest dimensions, to that of the next layer, and adding the two layers together. This procedure should be applied recursively, until the base is hit and all layers have been accumulated.
Mask generation
Once we have the Laplacian Pyramid, the only step remaining is to create an appropriate mask for blending the two images together. The mask will determine how natural the blend appears, as the mask will determine how much of each image to use per pixel location. The transformation is a simple weighted average, where \(\alpha\) determines the weighting. \[\alpha(image A) + (1-\alpha)(image B)\]
In order to create a blend that appears natural, a mask that allows for a smooth transition is necessary, thus a continuous function along a particular axis is desired as opposed to a step function. The sigmoid function is a decent starting point, as the input domain is squashed into the range of \(0\) to \(1\), which is exactly what we need. That said, the sigmoid function in its raw form results in a mask that is too “steep” of a slope, which will result in a rather abrupt transition from image A to image B.

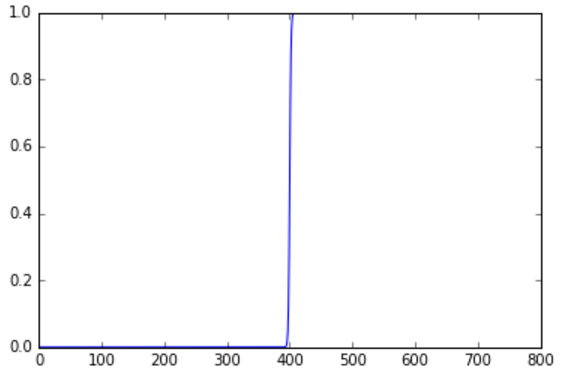
In order to mold the mask into something more applicable, we can add a “fatness” parameter to control the slope, and speed of the transition.

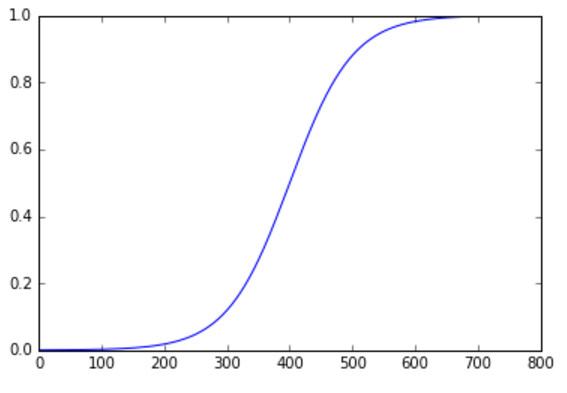
Just from the mask alone we can visually confirm the smooth transition from the left to the right side. Applying this kind of mask to blend each layer of the Laplacian results in rather favorable results. The masks can be quickly generated using the below functions written in python.
def sigmask(image):
r,c = image.shape
y = sp.special.expit(np.arange(-c//2,c//2))
return np.tile(y,(r,1))
def fatmask(image, fatness):
r,c = image.shape
y = map(lambda x: 1/(1+np.exp((1/float(fatness))*-x)), np.arange(-c//2,c//2))
return np.tile(y,(r,1))Hand-eye mask template
Now to produce the hand eye blend, we need a mask with the shape of an ellipse, or some shape that matches the general characteristics of the shape of a human eye, in addition to maintaining the above properties that results in a smooth transition. The 2D Gaussian function is close to ideal for generating a mask suitable for this particular task, with a greater deviation along the x-axis resulting in an elliptical shape resembling that of an eye.



Once we have the mask template in hand, we can generate the Gaussian Pyramid and apply the blending operation at each layer of the Laplacian, followed by the collapse of the pyramid to generate the final image. Note the images were rescaled for visualization. Each layer has successively smaller dimensions than the dimensions of the prior layer.
The blended result for each layer.

Final blended product
The final collapsed image.

(All mistakes are mine, any corrections appreciated.)
References:
- Burt, Peter J and Adelson, Edward H. A Multiresolution Spline with Application to Image Mosiacs
- Burt, Peter J and Adelson, Edward H. The Laplacian Pyramid as a Compact Image Code