This post is a quick summary of findings from working on assignment 1 from CS 294: Deep Reinforcement Learning, Spring 2017, open sourced by Berkeley. [1] Reviewing the material, I have to say the quality and depth is overwhelming, and despite being one sample, attests to the education provided by Berkeley and the professors employed. I envy the students that have the opportunity to engage and participate live in a course structured by Professor Levine and team. Making this lecture accessible is a great service, and I can only share my appreciation through a simple virtual “Thank you”.
source code: behavioral cloning
Problem Definition
In part 1 of the assignment, we are tasked with finding a policy for a selection of agents, with each agent having their own definition of an observation space, \(o \in R^{n_{o}}\), and action space, \(a \in R^{n_{a}}\),. The policy in the deterministic case is defined as \(a = \pi(o)\), and in the stochastic case is a distribution, \(\pi(a | o)\), over the observation space. We want to learn the policy that results in the largest return on evaluation, which in this case is defined as \(\sum_{t=0}^n r_t\), but difficult in practice. The lecture introduces the concept of behavioral cloning, which addresses the question, given examples derived from an expert, can we learn a sufficient policy. Note that I don’t describe the policy as optimal, as the policy learned is only good as the input, in other words the so called expert in this case. The expert can be formulated in many ways, such as human control, MPC (Model Predictive Control), or even a simple logic based control algorithm. Its clear the term expert is subjective, and we can easily see how the resulting policy learned is really only good as the expert provided.
For this particular case, an expert policy is provided, and we are essentially left to solve a supervised learning problem, finding the function approximator that best fits the given data, where the data is defined by the expert, and the amount of samples generated for training is specified by the user. The problem simplifies to a matching game, where we need to find and match the function approximator used by the expert.
Experimentation Hopper-v1

Wanting to start with a relatively easy environment provided by OpenAI gym, based on the simulation engine Mujoco, I chose the Hopper-v1 environment which is composed of an observation space of 11 dimensions and actions space of 3 dimensions. A simple 2 layer NN was constructed, with the hidden layer composed of 64 units, ReLU as the activation function, with the rest of the relevant parameters defaulted to the default values specified in Keras. Using a batch size of 128, and training on 10 epochs, we can see that the neural net is able to learn the policy of the expert given enough samples, where samples is defined as the number of roll outs. The only pre-processing done was a normalization of the data set, using the mean, \(\mu_{train}\) and standard deviation, \(\sigma_{train}\) of the training data, with the same normalization procedure used on the test set, using \(\mu_{train}\) and \(\sigma_{train}\). Further, to handle the edge case of a zero deviation, small gaussian noise was added to any zero-valued \(\sigma\). A quick exercise confirms the sensitivity to the amount of data, as we train on roll out samples of 5, 10, 20, 40, 200, and 400. Each roll out is of variable length but consists of multiple tuples of \((o,a)\). Provided enough data, the capacity of this neural network was sufficient to “clone” the policy implicit in the training data supplied by the expert.
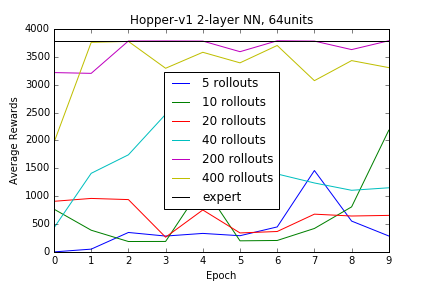
Experimentation Humanoid-v1

Lets see if we can try and generate a fail case. We can test the capacity of this particular neural net, on a more complex environment. The Humanoid-v1 seems to be a good test, with the environment consisting of an observation space of 376 dimensions, and action space of 17 dimensions. The capacity of the simple neural net was sufficient, provided that enough samples of the expert policy was supplied.
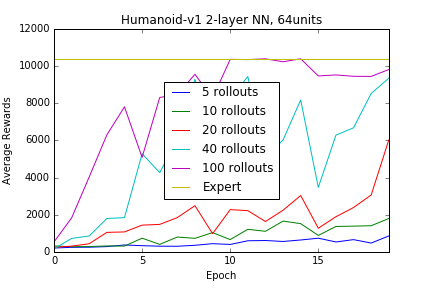
Just as an exercise we can increase the capacity of the model, using a deeper neural network defined by 2 hidden layers with 512 units each, with some regularization via dropouts (30%) after each layer, results in relatively satisfactory results, again given enough data, but such capacity is clearly unnecessary when given samples from an expert policy in this particular situation.
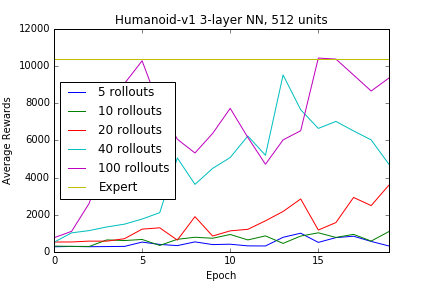
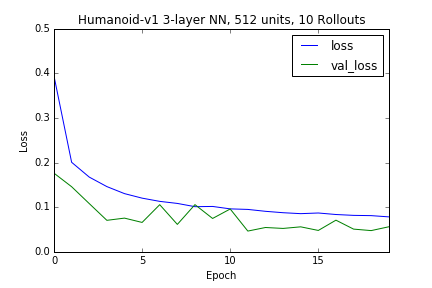
Conclusion:
In summary, access to enough data samples from an expert policy, and given a model with large enough capacity, we can find a pretty good policy that defines the actions at a given state, provided with a certain observation. The problem is finding that expert in the real world and collecting enough data samples to train a high capacity model.
(All mistakes are mine. Please kindly contact me on any mistakes found.)
Note:
- Hopper-v1 and Humanoid-v1 images credited to [2]
- Experiments were based on a trial version of Mujoco [3]
References
- Deep RL Assignment 1: Imitation Learning. http://rll.berkeley.edu/deeprlcourse/docs/hw1.pdf
- OpenAI, Hopper-v1. https://gym.openai.com/envs/Hopper-v1
- MuJoCo advanced physics simulation. https://www.roboti.us/index.html